3.4 Madde Analizi
Bir ölçme aracı geliştirme çalışmasında, ölçme aracının tümüne ait özelliklerin yanında o araçtaki maddelerin özellikleri de incelenmekte ve maddelerin istenilen özellikte olup olmadığı madde analizi ile belirlenmektedir. Madde analizinde bir maddenin güçlüğü, madde ayırıcılık gücü, madde standart sapması ve madde güvenirliği hesaplanabilir (Turgut & Baykul, 2010). Bu bölümde araştırmacıların sıklıkla başvurduğu iki madde istatistiği olan madde güçlük indeksi, madde ayırıcılık gücü indeksi ve madde güvenirliği ele alınmıştır.
3.4.1 Madde Güçlük İndeksi
Klasik test kuramına göre bir maddenin güçlüğü, o maddenin tüm grup tarafından doğru yanıtlanma oranı olarak ifade edilmekte ve p sembolü ile gösterilmektedir (Crocker & Algina, 2008). Madde güçlüğünün matematiksel gösterimi aşağıda verilmiştir (Turgut & Baykul, 2010):
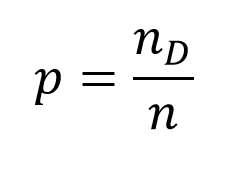
\(n_{D}:\) Maddeyi doğru yanıtlayan kişi sayısı
\(n:\) Toplam kişi sayısı
Yukarıdaki eşitlikten görülebileceği gibi, bir maddeyi kimsenin doğru yanıtlayamaması halinde p değeri 0.00 olurken, tüm katılımcıların doğru yanıtlaması durumunda p değeri 1.00 olur. Bu bağlamda, maddeyi daha az kişi doğru yanıtladıkça, yani p sıfıra yaklaştıkça ilgili madde güçleşirken; maddeyi daha çok kişi doğru yanıtladıkça, yani p 1’e yaklaştıkça ilgili madde kolaylaşmaktadır. Madde güçlüğü değerleri aşağıdaki gibi yorumlanabilir:
- 0.00 - 0.19: Çok zor
- 0.20 - 0.39: Zor
- 0.40 - 0.59: Orta güçlükte
- 0.60 - 0.79: Kolay
- 0.80 - 1.00: Çok kolay
Aşağıda farklı güçlük düzeylerine sahip maddeler oluşturulmuş ve madde güçlük düzeyleri hesaplanmıştır.
# Beş madde için 0-1 puan üretimi
set.seed(1234)
m1 <- sample(0:1, 50, replace = TRUE, prob=c(0.90,0.10) ) # Çok zor madde
m2 <- sample(0:1, 50, replace = TRUE, prob=c(0.75,0.25)) # Zor madde
m3 <- sample(0:1, 50, replace = TRUE, prob=c(0.50,0.50) ) # Orta güçlükte madde
m4 <- sample(0:1, 50, replace = TRUE, prob=c(0.25,0.75)) # Kolay madde
m5 <- sample(0:1, 50, replace = TRUE, prob=c(0.10,0.90)) # Çok kolay madde
# Maddelerden tek bir veri oluşturma
maddeler <- cbind(m1, m2, m3, m4, m5)
# Madde güçlüğü (Sütun ortalamaları madde güçlüğünü verecektir)
gucluk <- colMeans(maddeler) # Sütun ortalamaları
gucluk## m1 m2 m3 m4 m5
## 0.06 0.18 0.50 0.72 0.90Doğru yanıtın 1, yanlış ve boş yanıtlarınsa 0 olarak puanlandığı bir ölçme aracında, doğru yanıtlanma oranının hesaplanması oldukça basittir. Ancak açık uçlu madde gibi, puanlamanın 1-0 dışında yapıldığı durumlarda doğru yanıtlama oranı hesabı biraz farklılaşmaktadır. Bu durumda, maddenin ortalama puanı, madde ranjına bölünerek madde güçlük indeksi hesaplanabilir (Kilmen, 2014):
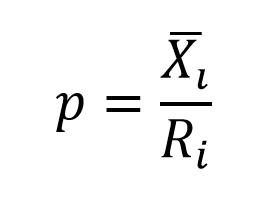
\(\overline{X_i}:\) Madde puan ortalaması
\({R_i}:\) Madde puan ranjı
Madde güçlüğü, maksimum performansın ölçülmediği Likert tipi ölçek maddelerine uygulanması halinde farklı bir anlam taşır. Madde Tepki Kuramına dayalı çalışmalarda Likert tipi ölçek maddeleri için de güçlük parametresi hesaplanmakta, ancak bu parametre belirli bir seçeneği onaylama güçlüğü olarak yorumlanmaktadır.
# Beş madde için 1-10 puan üretimi
m1 <- sample(1:10, 50, replace = TRUE)
m2 <- sample(1:10, 50, replace = TRUE)
m3 <- sample(1:10, 50, replace = TRUE)
m4 <- sample(1:10, 50, replace = TRUE)
m5 <- sample(1:10, 50, replace = TRUE)
# Maddelerden tek bir veri oluşturma
maddeler <- cbind(m1, m2, m3, m4, m5)
# Madde güçlüğü (Sütun ortalamalarının bir maddeden alınabilecek
# en yüksek puana bölümü madde güçlüğünü verecektir)
gucluk <- colMeans(maddeler) / 10 # En yüksek puan 10
gucluk## m1 m2 m3 m4 m5
## 0.526 0.554 0.520 0.580 0.510Aşağıda madde güçlüğünü hesaplayan basit bir Shiny uygulaması örneği verilmiştir:
Veri yükleme butonundan “sav” uzantılı (SPSS) 1-0 şeklinde puanlanmış bir dosya yükleyiniz.
Çıktıda maddelere ilişkin güçlük düzeyleri yer almaktadır. Shiny uygulamasının bulunduğu pencerenin sağ tarafında bulunan çubuğu aşağı çekerek tüm analiz sonuçlarını görebilirsiniz. Madde sayısı 25’ten fazlaysa çıktı tablosunun altında yer alan “next” butonuna basarak diğer maddelere ilişkin madde güçlük düzeylerini görebilirsiniz.
3.4.2 Madde Ayırıcılık Gücü İndeksi
Ölçme aracında yer alacak maddelerin, ölçülmek istenilen özellik bakımından düşük ve yüksek düzeydeki bireyleri ayırabilmesi istenir. Madde ayırıcılık gücü indeksi, ölçülen özelliği düşük ve yüksek olan bireyleri ne derece ayırabildiğini gösteren bir istatistiktir. Temelde madde puanlarıyla ile toplam puan arasındaki korelasyonu ifade eder (Baykul, 2010).
Madde ayırıcılık gücü indeksinin tanımı dolayısıyla madde puanları ile toplam puanlar arasındaki korelasyon katsayısının hesaplanması gerekmektedir. Maddelerin 1-0 şeklinde puanlandığı durumlarda, madde puanı süreksiz; toplam puan ise sürekli bir değişkendir. Dolayısıyla iki kategorili süreksiz bir değişken ile sürekli bir değişken arasındaki korelasyon katsayısının hesaplanması gerekmektedir. Bu amaca uygun olarak çift serili ve nokta çift serili korelasyon katsayıları öne çıkmaktadır.
Çift serili korelasyon katsayısında, iki kategorili süreksiz değişkenin yapay süreksiz olduğu kabul edilmektedir. Yani aslında sürekli olan bir değişken, yapay olarak 1 ve 0 değerlerine dönüştürülmüştür. Bireylerin bir madde ile ölçülen özelliklerinin normal dağılım gösteren ve -\(\infty\) ile +\(\infty\) arasında değiştiği kabulü dikkate alınırsa, birey yanıtlarının sürekli bir değişken iken, yapay olarak 1 ve 0 değerlerine dönüştürüldüğü varsayılabilir. Bu durumda madde ve toplam puanlar arasındaki korelasyonun hesaplanmasında en uygun yöntem çift serili korelasyon katsayısıdır. Bu katsayı aşağıdaki formüller hesaplanabilir (Baykul, 2010):
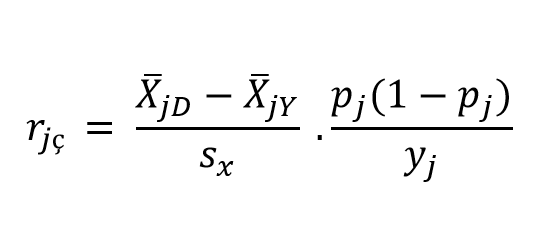
\(\overline{X_{jD}}:\) Maddeyi doğru yanıtlayanların ortalaması
\(\overline{X_{jY}}:\) Maddeyi yanlış yanıtlayanların ortalaması
\(s_{x}:\) Testin standart sapması
\(p_{j}:\) Madde güçlüğü
\(y_{j}:\) Normal dağılım eğrisi altında kalan alanın sağ uçtan itibaren \(p_{j}\) kadarını ayıran ordinat.
Nokta çift serili korelasyon katsayısı ise süreksiz olan değişkenin yapay olarak değil gerçekte iki kategorili olduğunu kabul etmektedir. Madde yanıtlarının gerçekte süreksiz ve 1 - 0 şeklinde olduğu varsayımı ile hareket edilirse, madde ve toplam puanlar arasındaki korelasyon nokta çift serili korelasyon katsayısı ile hesaplanmalıdır. Nokta çift serili korelasyon katsayısı aşağıdaki eşitlikle hesaplanabilir (Baykul, 2010):
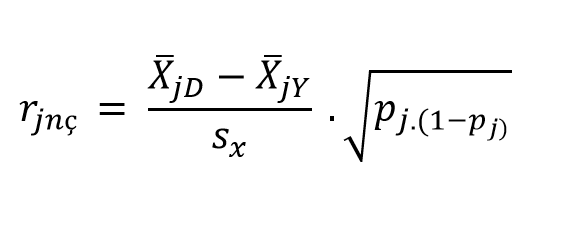
\(\overline{X_{jD}}:\) Maddeyi doğru yanıtlayanların ortalaması
\(\overline{X_{jY}}:\) Maddeyi yanlış yanıtlayanların ortalaması
\(s_{x}:\) Testin standart sapması
\(p_{j}:\) Madde güçlüğü
Madde ayırıcılık gücü indeksinin hesaplanmasında, alt ve üst gruplar yöntemi de kullanılabilmektedir. Bu yöntemde yanıtlayıcı grup toplam puana göre başarı sırasına dizilir. En başarılı %27’lik grup ile en başarısız %27’lik grup kullanılarak aşağıdaki eşitlikten yararlanılır:
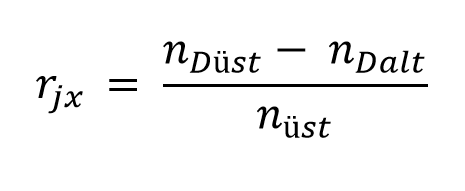
\(n_{Düst}:\) Üst gruptan maddeye doğru yanıt verenlerin sayısı
\(n_{Dalt}:\) Alt gruptan maddeye doğru yanıt verenlerin sayısı
\(n_{üst}:\) Üst gruptaki toplam kişi sayısı. (Bunun yerine alt gruptaki toplam kişi sayısı da kullanılabilir)
Bu eşitliğe göre, başarılı öğrencilerin maddeyi doğru; başarısız öğrencilerinse yanlış yanıtlama miktarı arttıkça, maddenin başarılı ve başarısız öğrenciyi ayırma gücü artacak, dolayısıyla ayırıcılık gücü indeksi de büyüyecektir. Bu yöntem veri kaybına neden olduğu için çift serili ve nokta çift serili korelasyon katsayılarının kullanımı daha doğru olacaktır. Eğer elinizde büyük bir veri seti varsa ve korelasyon katsayılarının hesaplanmasını kolaylaştıracak bilgisayar yazılımı mevcut değilse bu yöntem kullanılabilir.
1-0 şeklinde puanlanmayan maddeler için madde ayırıcılık gücü indeksi ise yine korelasyon katsayısından yararlanılarak hesaplanabilir. Bu amaçla Pearson momentler çarpım korelasyon katsayısı ya da Spearman sıra farkları korelasyon katsayısının kullanılması mümkündür. Seçilecek yöntem, araştırmacının madde puanlarının sıralama düzeyinde mi yoksa eşit aralıklı düzeyde mi varsayacağına göre değişmektedir. Pearson momentler çarpım korelasyon katsayısı her ikisi de en az eşit aralık düzeyinde ölçülmüş iki değişken arasındaki ilişkinin belirlenmesinde kullanılmaktadır. Örneğin, Likert tipi bir maddenin eşit aralıklı düzeyde yanıtlandığı varsayılıyorsa (bunun üzerine farklı görüşler mevcuttur ve tartışmalı bir konudur), madde-toplam korelasyonunun hesaplanmasında Pearson momentler çarpım korelasyon katsayısından yararlanılabilir. Aksine, maddelere verilen yanıtların sıralama düzeyinde olduğu kabul ediliyorsa Spearman sıra farkları korelasyon katsayısı kullanılarak, madde ayırıcılık gücü indeksinin hesaplanması mümkündür.
Madde ayırıcılık gücü indeksi bir korelasyon katsayısı olduğu için -1 ile +1 arasında değerler alır. Madde ayırıcılık gücü indeksinin negatif değer alması, maddenin ölçülen özellik bakımından yüksek ve düşük düzeydeki kişileri ters ayırt ettiğini gösterir. Başka bir deyişle, düşük düzeydekiler bir maddeye doğru / olumlu yönde yanıt verirken; yüksek düzeydekiler yanlış / olumsuz yönde yanıt vermektedir. Özellikle Likert tipi maddelerde bu durumla karşılaşılması durumunda, maddenin ters kodlanmasının gerekip gerekmediği incelenmelidir. Başarı testlerinde ise cevap anahtarının yanlış kodlanıp kodlanmadığı kontrol edilmelidir. Ayırt edicilik düzeyi negatif çıkan başarı testindeki bir madde için “soruda bilen öğrencinin kafasını karıştıran, bilmeyen öğrenciye ise ipucu veren” unsurların olup olmadığı incelenmelidir.
Madde ayırıcılık gücü indeksi aşağıdaki gibi yorumlanabilir:
- 0.40 ve üzeri: Çok iyi madde
- 0.30 - 0.39: İyi madde, ancak geliştirilebilir
- 0.20 - 0.29: Düzeltilmesi gereken madde
- 0.00 - 0.19: Düzeltilemiyorsa testten çıkarılması gereken madde
- Negatif: Bireyleri ters ayıran madde. İfade veya yanıt anahtarı kontrol edilmelidir.
# Beş madde için 0-1 puan üretimi
m1 <- sample(0:1, 50, replace = TRUE)
m2 <- sample(0:1, 50, replace = TRUE)
m3 <- sample(0:1, 50, replace = TRUE)
m4 <- sample(0:1, 50, replace = TRUE)
m5 <- sample(0:1, 50, replace = TRUE)
# Maddelerden tek bir veri oluşturma
maddeler <- cbind(m1, m2, m3, m4, m5)
# Toplam puanı hesaplama
toplam <- rowSums(maddeler) # Satır toplamı
# Madde ayırt edicilik gücü (Madde - toplam korelasyonu)
ayirt.edicilik <- NULL # Döngü içinde çağıracağımız değişkeni oluşturuyoruz
for(i in 1:ncol(maddeler)){ # 1'den madde sayısı kadar yap
# i. madde ile toplam puan arasındaki korelasyonu hesapla
ayirt.edicilik.tmp <- polycor::polyserial(maddeler[,i], toplam)
# i. maddenin ayırt ediciliği ile diğer maddelere ait
# ayırt edicilik indekslerini birleştir.
ayirt.edicilik <- cbind(ayirt.edicilik, ayirt.edicilik.tmp)
}
# Sütun isimlerini düzenle
colnames(ayirt.edicilik) <- c("rjx1", "rjx2", "rjx3", "rjx4", "rjx5")
round(ayirt.edicilik, 2) # Virgülden sonra iki basamağa yuvarla## rjx1 rjx2 rjx3 rjx4 rjx5
## [1,] 0.29 0.45 0.56 0.5 0.33Aşağıda madde ayırt ediciliğini hesaplayan basit bir Shiny uygulaması örneği verilmiştir:
Veri yükleme butonundan “sav” uzantılı (SPSS) 1-0 şeklinde puanlanmış bir dosya yükleyiniz.
Çıktıda maddelere ilişkin çift serili ve nokta çift serili korelasyon katsayıları yer almaktadır. Shiny uygulamasının bulunduğu pencerenin sağ tarafında bulunan çubuğu aşağı çekerek tüm analiz sonuçlarını görebilirsiniz. Madde sayısı 25’ten fazlaysa çıktı tablosunun altında yer alan “next” butonuna basarak diğer maddelere ilişkin madde ayırt edicilik düzeylerini görebilirsiniz.
3.4.3 Madde Güvenirliği
Madde güvenirliği, madde varyansı ve madde-toplam korelasyonu kullanılarak elde edilen değerlerdir (Crocker ve Algina, 2008). Bu değer \(\sigma\).r\(_{pb}\) ile hesaplanmaktadır. j, madde numarası olmak üzere; \(\sigma_{j}\), madde standart sapmasını, r\(_{jx}\) ise madde ayırıcılık gücü indeksini temsil etmektedir. Madde standart sapması, madde varyansının kareköküdür. Madde varyansı ise madde güçlüğünün bir fonksiyonudur:
\(\sigma_{j}\) = \(\sqrt{p_{j}q_{j}}\)
\(p_{j}\); j. maddenin madde güçlüğünü temsil ederken, \(q_{j}\) ise 1 - \(p_{j}\)’dir. Dolayısıyla bir maddeye ait madde güçlüğü ile (1 - madde güçlüğü)’nün çarpımı madde varyansını; bu değerin karekökü ise madde standart sapmasını vermektedir.
Madde güvenirliği, özellikle test güvenirliğini yükseltecek maddelerin testte kalmasının istendiği durumlarda kullanışlıdır. Örneğin iki maddeye ait ayırıcılık gücü indeksi 0.60 olsun. Ancak ilk maddenin güçlük indeksi 0.20, ikinci maddenin güçlük indeksi ise 0.50 olsun. Bu iki maddeden madde varyansı büyük olanın, madde güvenirliği de büyük olacaktır. Bu bağlamda yüksek güvenirlikli bir test için varyansı büyük olan maddenin seçilmesi gerekecektir. Her iki durum için madde güvenirliği hesaplanırsa:
- madde (\(p_{1}\) = .20, \(r_{1x}\) = 0.50) için güvenirlik: \(\sqrt{0.20(1-0.20)}0.50 = 0.20\)
- madde (\(p_{2}\) = .60, \(r_{2x}\) = 0.50) için güvenirlik: \(\sqrt{0.60(1-0.40)}0.50 = 0.25\)
Bu örnekte, 2. maddenin test güvenirliğine katkısı, 1. maddeye göre daha fazla olacaktır.
Bu bölümde KTK ana hatları ile ele alınmıştır. Daha ayrıntılı bilgi için (Algina & Crocker, 1986; Baykul, 2000) kaynaklarının incelenmesi önerilir.